本题来自力扣第50题,题目不复杂，就是计算xⁿ https://leetcode-cn.com/problems/powx-n/ 。难度：简单

先看题目

第一眼看到这个题的时候我的表情是这样的

我寻思着不就一行代码解决的事情么

x**n

可它的难度是中等，肯定不止这么沙雕。

既然解决很简单那么肯定就要高效

想想看怎么才能优化代码呢？

这样暴力的话时间复杂度是O(n)

有没有更快的方法呢？

答案是：快速幂

可以递归求解，但是我比较讨厌递归因为它会占很多空间

所以就看看其中的另一种实现方式

分而治之

比如

2¹⁰=2^2x5=(2²)⁵

想想看着有什么用呢？

2¹⁰是10个2相乘

但是

(2²)⁵

是5个4相乘

循环次数直接少了一半

这个可以直接折半是因为n是偶数

那如果n是奇数呢？

只需要把n想办法变成偶数就行

方法就是乘出去一个x

(2²)⁵=(2²)⁴*x

这样的话如果n永远是偶数，直接一直折半就变成了x的1次幂

但是事实是折半几次后n就会变成奇数

12//2=6 6//2=3

10//2=5

奇数就多乘若干个x就行，因为每次都会分出去一个多余的x

当n为偶数处理最后一步折半成x¹

这时候，n为奇数再分出去一个x

所以最后的结构类似于(res就是每次n为奇数的时候分出去的)

x⁰ * res

类似于降档（幂）补油(x)的操作

比如

3⁵

刚开始就可以看成 3⁵ *res (此时res=1)

最后一步左边是一个数的0次幂=1所以

最后的结果就是res的值了

那如果n是负数呢？

2² = (½)²

只需把x换成1 / x;n换成-n算就行

处理特殊情况

如果给定的x为0

那么直接返回0就行

因为

数字 00 的正数次幂恒为 00；00 的 00 次幂和负数次幂没有意义，因此直接返回 0 即可。

代码时刻

    def myPow(self, x: float, n: int) -> float:
   
     if x == 0.0: return 0.0
        res = 1
        if n < 0: x, n = 1 / x, -n
        while n:
            if n & 1: res *= x      #n&1是二进制操作，按位与，等同于n%2==1判断n是否为奇数,是的话执行res=res*x
            x *= x					#不是的话x=x*2, 比如：9**2*(1*3)=81*(1*3)  左边x=9右边x=81并且降幂了，降幂操作在下一步
            n >>= 1					#偶数的话每次将n折半，等同于 n=n//2 ">>"是二进制里右移一位,十进制里右移相当于除以10
            						#那么二进制里右移就是除以2喽

效率对比

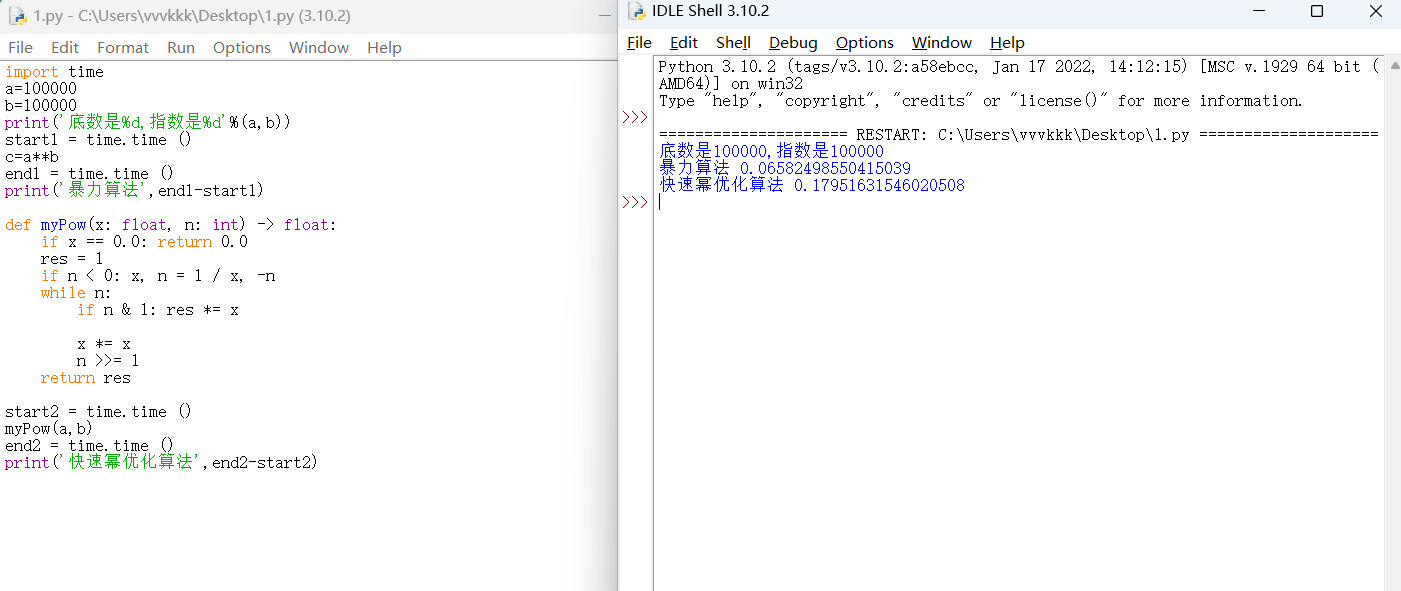
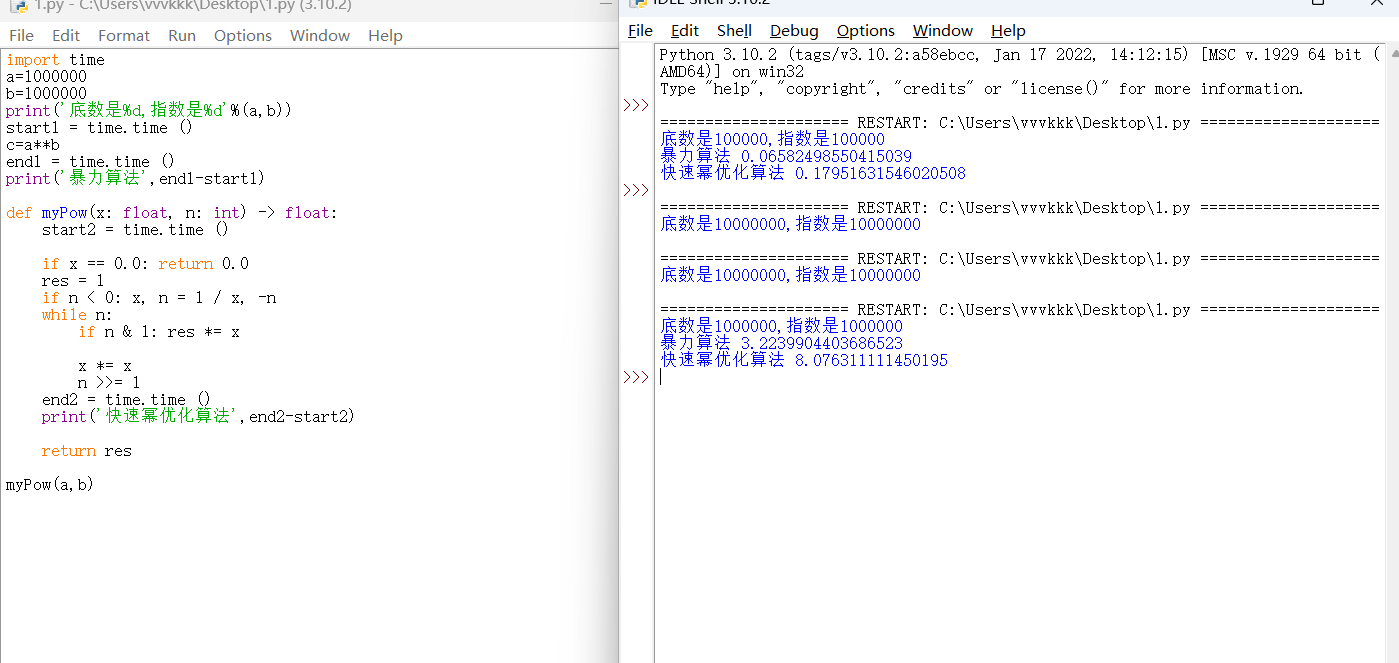
奶奶的腿，优化了个寂寞，反而更慢了

哪位大佬能告诉我这是为啥？？？